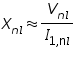LIST OF SYMBOLS

f_r  =  rated electrical frequency of the motor

V_1,rl   =   the line-to-neutral voltage

l_1,rl   =   the line current

P_nl  =  the poly-phase electrical input power

I²R  =  no-load rotor loss

P_rot  =   rotational loss

J  =  rotor Inertia

n_ph  =  number phase

w_m  =  rotor speed

T_rot  =  rotor torque

R_c  =  core loss resistance

P_core  =  no-load core loss

S_nl  =  total apparent power input at no load

R₁  =  resistance of the motor

X₁  =  reactance of the motor

X₂  =  rotor leakage reactance

X_m  =  megnetizing reactance

X₁₁  =  self-reactance of the rotor

X_nl  =  apparent reactance

Q_nl  =  reactive power at no load

THEORY

The no load test on an induction motor gives information with respect to exciting current and no-load losses. The test is performed at rated frequency and with balanced poly-phase voltages applied to the stator terminals. Readings are taken at the rated voltage, after the motor runs long enough for the bearings to be properly lubricated.

At no load, the rotor current is only the very small value needed to produce sufficient torque to overcome the friction and windage losses associated with rotation. The no-load rotor I²R loss is, therefore, negligibly small. Unlike the continuous magnetic core in a transformer, the magnetizing path in an induction motor includes an air gap which significantly increases the required exciting current. Thus, in contrast to the case of a transformer, whose no-load primary I²R loss is negligible, the no-load stator I²R loss of an induction motor may be appreciable because of this larger exciting current. Neglecting rotor I²R losses, the rotational loss P_rot for normal running conditions can be found by subtracting the stator I²R losses from the no-load input power.

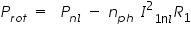
The total rotational loss at rated voltage and frequency under load usually is considered to be constant and equal to its no-load value.

Various tests can be performed to separate the friction and windage losses from the core losses. For example, if the motor is not energized, an external drive motor can be used to drive the rotor to the no-load speed and the rotational loss will be equal to the required drive-motor output power. Alternatively, if the motor is operated at no load and rated speed and if it is then suddenly disconnected from the supply, the decay in motor speed will be determined by the rotational loss as

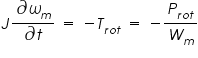
Hence, if the rotor inertia J is known, the rotational loss at any speed wm can be determined from the resultant speed decay as

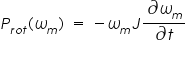
Thus, the rotational losses at rated speed can be determined by evaluating the above equation as the motor is first shut off when it is operating at rated speed. If the no-load rotational losses are determined in this fashion, the core loss can be determined as

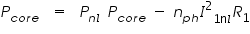
Here, P_core is the total no-load core loss corresponding to the voltage of the no-load test (typically rated voltage). Under no-load conditions, the stator current is relatively low and, to a first approximation, one can neglect the corresponding voltage drop across the stator resistance and leakage reactance. Under this approximation, the voltage across the core-loss resistance will be equal to the no-load line-to-neutral voltage and the core-loss resistance can be determined as

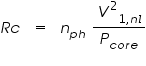
Provided that the machine is operated close to rated speed and rated voltage, the refinement associated with separating out the core loss and specifically incorporating it in the form of a core-loss resistance in the equivalent circuit will not make a significant difference in the results of an analysis. Hence, it is common to ignore the core-loss resistance and to simply include the core losses with the rotational losses.

Because the slip at no load, S_nl, is very small, the reflected rotor resistance R₂/S_nl is very large. The parallel combination of rotor and magnetizing branches then becomes jX_m shunted by the rotor leakage reactance X₂ in series with a very high resistance, and the reactance of this parallel combination therefore very nearly equals X_m .Consequently the apparent reactance X_nl measured at the stator terminals at no load very nearly equals X₁ + X_m, which is the self-reactance X₁₁ of the stator; i.e.

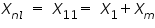
The self-reactance of the stator can therefore be determined from the no-load measurements. The reactive power at no load Q_nl can be determined as

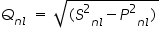
where S_nl = n_ph V_1,nl I_1,nl is the total apparent power input at no load.

The no-load reactance X_nl can then be calculated from Q_nl and I_nl as

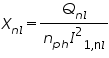
Usually the no-load power factor is small ( i.e., Q_nl >> P_nl ) so that the no-load reactance very nearly equals the no-load impedance.